Simple Example Showing UQ With PCE¶
This example shows some basic functionality of UncertainSCI using the polynomial Chaos emulators (PCE) to quantify uncertainty in a 1D function. It is essentially identical to demos/build_pce.py and uses a 1D Laplacian ODE as a model with three parameters
[1]:
import numpy as np
from matplotlib import pyplot as plt
from UncertainSCI.distributions import BetaDistribution
from UncertainSCI.model_examples import laplace_ode_1d
from UncertainSCI.pce import PolynomialChaosExpansion
from UncertainSCI.vis import piechart_sensitivity, quantile_plot, mean_stdev_plot
Model Parameter setup¶
The first step in running UncertainSCI is to specify the parameter distributions and the capacity of the PCE model (polynomial order).
Distributions¶
[2]:
# Number of parameters
Nparams = 3
# Three independent parameters with different Beta distributions
p1 = BetaDistribution(alpha=0.5, beta=1.)
p2 = BetaDistribution(alpha=1., beta=0.5)
p3 = BetaDistribution(alpha=1., beta=1.)
plabels = ['a', 'b', 'z']
Polynomial Order¶
How complicated the model is
[3]:
# # Polynomial order
order = 5
Forward Model¶
with \(x\) in \([-1,1]\) discretized with \(N\) points, where \(a(x,p)\) is a Fourier-Series-parameterized diffusion model with the variables \(p_j=[a, b, z]\). See the laplace_ode_1d method or UncertainSCI/model_examples.py for details.
[4]:
N = 100
x, model = laplace_ode_1d(Nparams, N=N)
Running PCE in UncertainSCI¶
The steps to running PCE in UncertainSCI are - create PCE object - generate parameter samples - run parameter sets in the forward model - give model output to PCE - compute output statistics
Create PCE object and Build Sample Set¶
With the parameter distribution created and polynomial order set, we can create the PCE object and generate a parameter set that will efficiently and accurately estimate the output distribution of the model. UncertainSCI adds an extra 10 parameter sets as a precaution.
[5]:
pce = PolynomialChaosExpansion(distribution=[p1, p2, p3], order=order, plabels=plabels)
pce.generate_samples()
print('This queries the model {0:d} times'.format(pce.samples.shape[0]))
Precomputing data for Jacobi parameters (alpha,beta) = (-0.500000, 0.000000)...Done
This queries the model 66 times
Run Parameter Sets in the Forward Model¶
We query each parameter set in sequence to run in our Laplacian ODE model and collect the results
[6]:
model_output = np.zeros([pce.samples.shape[0], N])
for ind in range(pce.samples.shape[0]):
model_output[ind, :] = model(pce.samples[ind, :])
Build PCE from Model Outputs¶
With the collated model solutions, the output distributions can be estimated using PCE
[7]:
pce.build(model_output=model_output)
[7]:
array([1.75571628e-37, 5.64860235e-17, 2.10743598e-16, 4.30180091e-16,
6.73615485e-16, 8.98426649e-16, 1.06808811e-15, 1.15833221e-15,
1.16057868e-15, 1.08209494e-15, 9.43231789e-16, 7.72726181e-16,
6.02299430e-16, 4.61625174e-16, 3.74362183e-16, 3.55551159e-16,
4.10403164e-16, 5.34387196e-16, 7.14489737e-16, 9.31478341e-16,
1.16290358e-15, 1.38643597e-15, 1.58302359e-15, 1.73934375e-15,
1.84914225e-15, 1.91328322e-15, 1.93860602e-15, 1.93592175e-15,
1.91761943e-15, 1.89536658e-15, 1.87829599e-15, 1.87191182e-15,
1.87777401e-15, 1.89387162e-15, 1.91549769e-15, 1.93639635e-15,
1.94995954e-15, 1.95029022e-15, 1.93300605e-15, 1.89571844e-15,
1.83817752e-15, 1.76211869e-15, 1.67087823e-15, 1.56886365e-15,
1.46096875e-15, 1.35201633e-15, 1.24629417e-15, 1.14722754e-15,
1.05720583e-15, 9.77557484e-16, 9.08648189e-16, 8.50065649e-16,
8.00849025e-16, 7.59724059e-16, 7.25312441e-16, 6.96294722e-16,
6.71517851e-16, 6.50048858e-16, 6.31183955e-16, 6.14427000e-16,
5.99452329e-16, 5.86065283e-16, 5.74169862e-16, 5.63747820e-16,
5.54848130e-16, 5.47581156e-16, 5.42108762e-16, 5.38620514e-16,
5.37288102e-16, 5.38194279e-16, 5.41239598e-16, 5.46038218e-16,
5.51822165e-16, 5.57379403e-16, 5.61052914e-16, 5.60824129e-16,
5.54493189e-16, 5.39951481e-16, 5.15520386e-16, 4.80308188e-16,
4.34519740e-16, 3.79646212e-16, 3.18469931e-16, 2.54843985e-16,
1.93246402e-16, 1.38157999e-16, 9.33612879e-17, 6.12921066e-17,
4.25845893e-17, 3.59260824e-17, 3.82825975e-17, 4.54770963e-17,
5.30202417e-17, 5.70278062e-17, 5.50298773e-17, 4.64948566e-17,
3.29537537e-17, 1.77021507e-17, 5.15427668e-18, 0.00000000e+00])
Compute Output Statistics¶
With the PCE built, statistics can be calculated for each point in the solution space (x).
[8]:
## Postprocess PCE: statistics are computable:
mean = pce.mean()
stdev = pce.stdev()
global_sensitivity, variable_interactions = pce.global_sensitivity()
quantiles = pce.quantile([0.25, 0.5, 0.75]) # 0.25, median, 0.75 quantile
Output Visualizations¶
To help understand and interpret UQ statistics, we’ve included some plotting tools for 1D data.
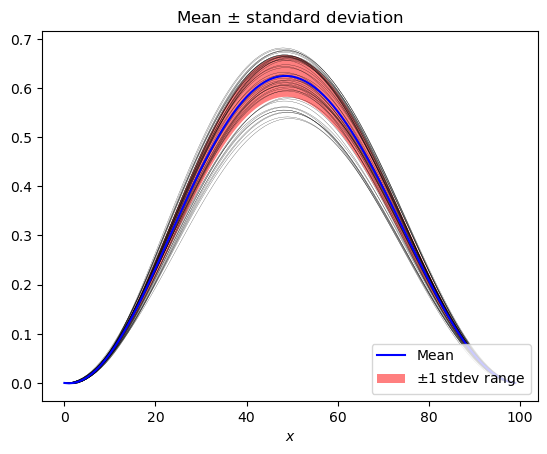
[9]:
mean_stdev_plot(pce, ensemble=50)
[9]:
<AxesSubplot:title={'center':'Mean $\\pm$ standard deviation'}, xlabel='$x$'>
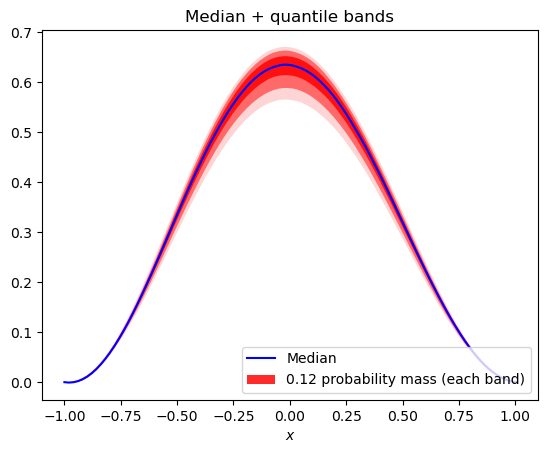
[10]:
quantile_plot(pce, bands=3, xvals=x, xlabel='$x$')
[10]:
<AxesSubplot:title={'center':'Median + quantile bands'}, xlabel='$x$'>
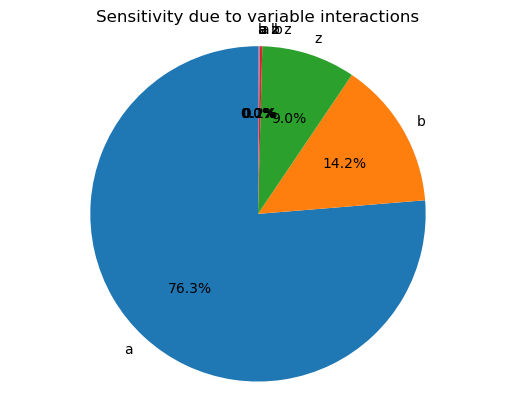
[11]:
piechart_sensitivity(pce)
[11]:
<AxesSubplot:title={'center':'Sensitivity due to variable interactions'}>